 NA-MIC Project Weeks
NA-MIC Project Weeks
Back to Projects List
Principal Axis Transform
Key Investigators
- Tina Wu (Sunnybrook Health Science Centre)
Acknowledgement
- Michael Hardisty (Sunnybrook Health Science Centre)
- Andras Lasso (Perk Lab)
- Andrew Yang
Project Description
Current slicer modules for general registration (BRAINs or Elastix) are unable to handle large initial mismatch between the two objects of interest. The purpose of this project is to create a slicer module that would allow registering two volumes with large initial mismatches (>15-20 degs) based on their principal axes. The module would also come with the capability for allowing users to visualize the volumes (as a model) and the direction of the principal vectors.
Objective
- Implement algorithm for performing principal axis transformation.
- Implement visualization tools.
Approach and Plan
- Load the CT scans
- Threshold the scans
- Find the inertial matrices associated with the two volumes
- Obtain the eigen vectors associated with the inertial matrices
- Calculate the transformation matrix
- Create models from the the initial scans
- Transform the center of the model to the world origin
- Apply the transform obtained from #5
- Create ruler annotations for visualizing the vectors and applying appropriate transformations (from #7 then #5)
Progress and Next Steps
The approach listed above was implemented but there are a few bugs, potentially due to the coordinate system mismatch between slicer/numpy/vtk. The goal during this week is to fix these and optimize the module.
End results:
- the volumes now align for small rotations; for large rotations, the principal axes might still be pointing in the opposite directions
- optimization
- spherical approximation integration
Future improvements:
- did not get a chance to implement visualization
- did not test it out on actual data
- did not implement proper logic class, so the module is not accessible through other modules
- did not investigate further why the crude axis correction mechanism did not work; did not implement the manual correction features
Illustrations
At the beginning of the week, the volumes look like this:
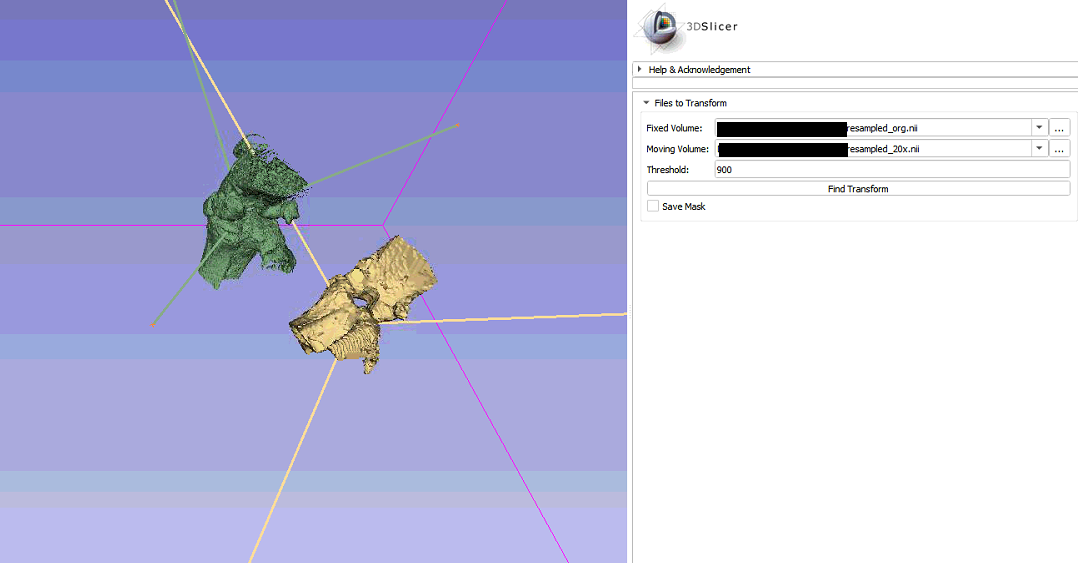
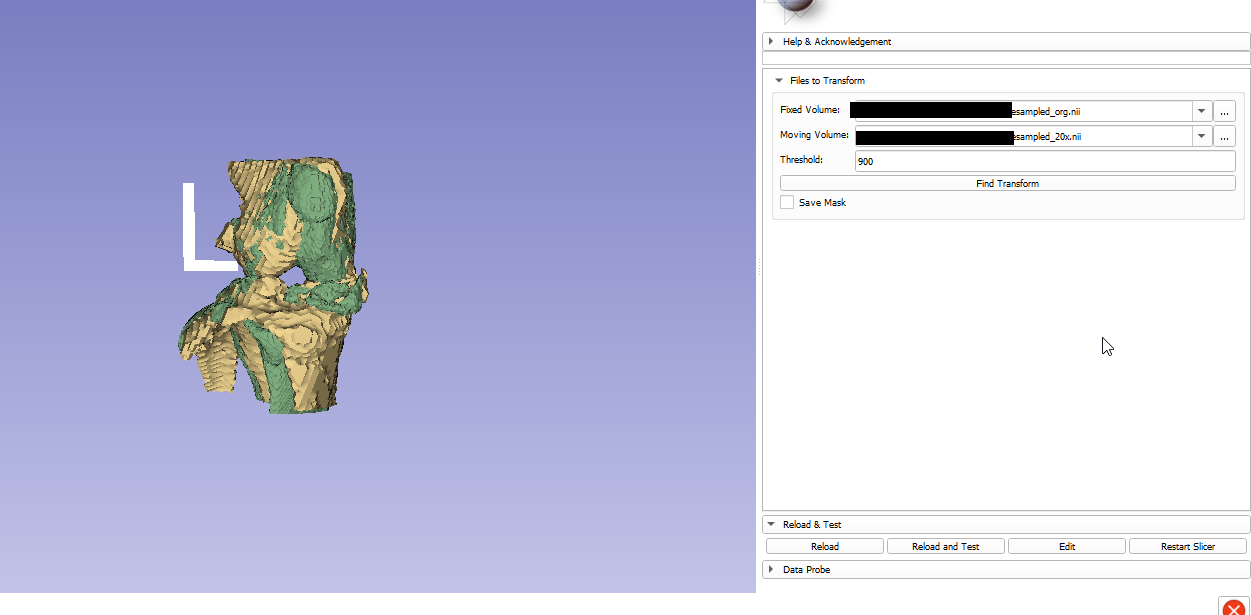
After the project week, the same volumes in the image above look like this:
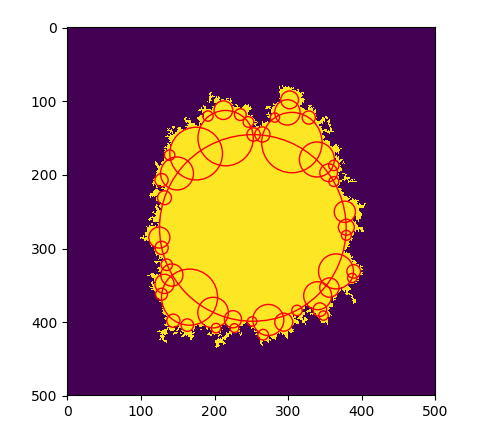
Progress on analysis:
Background and References
paper: http://jnm.snmjournals.org/content/31/10/1717.full.pdf
- Source code: https://bitbucket.org/blackfish03/paxistransform/src
- Test data: https://drive.google.com/open?id=1KaZk2cU_w5bR5BxWTUorOXIp1BnFHKfB